One approach to solve the mentioned two problems is dynamic network design, a branch of mathematical modeling describing problems in combinatorial graphs with a time dimension. Mathematically, pandemics are usually described by compartmental models such as the SIR model, which divides the population into three (or more) groups (susceptible, immune and removed) and calculates the dynamics of the number of occupants in each compartment over time by solving a set of differential equations or by discrete event simulation. Specialized software for both variants exists.

The idea to use disjoint compartments and discrete time intervals is at least one hundred years old (see for instance [2]) and is still subject to research (se for instance [3]). What we present here, and what is to some extent novel, is to demonstrate the flexibility and power of modern network design software in the form of Ab Ovo’s Network Designer when applied to model a pandemic.

Initially, Ab Ovo’s Network Designer was designed to optimize multi-commodity flows in logistics networks over time. Network Designer was used to model empty wagon repositioning, reusable container flows, supply chains in finished vehicle logistics, yard capacity in harbors, and much more. It turned out that the underlying mathematical model can also be used to support decision making in the management of a pandemic, as it is capable to cover all essential components of such a model, with the additional benefit of supporting an easy extension with further decision support functionality. Moreover, as Network Designer is equipped with a solver engine, such decisions can be optimized to alleviate the worst effects of the pandemic.

In the following, we demonstrate an experimental Network Designer model for the management of the COVID-19 pandemic.

Network Designer

Network Designer permits to specify dynamic flows in networks (see [1] for a survey), i.e. in networks where arcs have both capacities and durations. That is, if there is an arc in the network which starts in period 5 and which has a duration of 3, then the flow over this arc arrives at its destination in period 8.

For the pandemic model we associate the compartments of the population with nodes, and the arcs describe the transitions between them. The (single) commodity is the population and the flow equals the number of people who leave one compartment in one period to enter another compartment in another (usually the next) period.

The transition rates are taken from existing actuals and comprise usually of simple fractions of certain compartment counts in the previous period. One significant exception is how newly infected people are modeled within the experimental model, as their transition rates depend on the progress in the disease of the contacts which infected them.

The initial values of the compartment counts are also taken from actuals.

A key feature of the experimental model is the addition of compartments for affected persons and their state over time, i.e. there are different compartments for critically ill persons in week 2 after their infection in period p and critically ill persons in week 3 after their infection in period q. The model is sketched below.

All flows in nodes satisfy flow conservation. i.e., the inbound flow equals the outbound flow in each node which is neither source nor sink. All arcs marked with a Greek letter have additional constraints imposed on them governing the resulting flow, in the easiest case being a fraction of the flow into the preceding node. In other cases, the flow on one arc depends on the flow over one or more other arcs, not necessarily being incident to the arc in question.

Note that most of the flow within the substructure is determined by flow conservation and the additional constraints imposed on the flow. The rest is taken care of by the cost function which penalizes fatalities. In other experiments, we added the option to vaccinate a certain number of persons per period. Not surprisingly the model opted to vaccinate as many as possible to minimize fatalities. However, in the experiment described below, we omitted this option, for reasons stated later.

Some simplifying assumptions are made, like for instance a constant population, or that patients in intensive care do not spread the virus, whereas infected persons not in intensive care do for a couple of periods. The model is set up for a period duration of one week, since most statistical data is available for this granularity.

Each substructure described above is embedded into the network once for each period.

Experimental data and results

For our experiments we used data around December 18, 2020, from Bremen, Hamburg, Lower Saxony, North-Rhine-Westphalia and Schleswig-Holstein, the north-western federal states of Germany, comprising around 40% of the German population. At that time Germany was already under partial lockdown for some weeks, with a hard lockdown announced for the week before Christmas. In particular, the multiplication factors were taken from two weeks before December 19, which already showed some effect of these restrictions.

We included for each state an intensive care capacity and arcs which permit shuttling from one state to another if need be, with the intent of investigating whether these capacities are likely to be met in the near future. A consequence of the model is that the nodes describing the compartments with patients in intensive care are subdivided into one for each state and period.

Vaccinations, which are to start on December 27 in Germany, are not modeled, but could be easily included. We left them out since the exact number of vaccinations per period is not known yet, and the German policy of vaccinating elderly and otherwise highly vulnerable people first is not reflected in the model at all.

A sample of a network is shown below. The substructures are identifiable in the graph pane, each obtaining flow from their respective Susceptible node in their respective period, and releasing flow to nodes for recovered (V) and deceased (F).

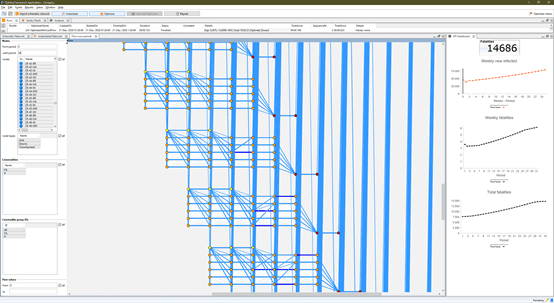
The model shows that after a few weeks shuttling traffic starts taking place (seen above as blue diagonal arcs between orange nodes), as some states reach the limit of their intensive care capacity (horizontal arcs between orange nodes in a darker blue shade), but fatalities because of this are not present for the first months.

Not only fatalities due to lack of intensive care capacity are expected, but the model can also be amended to answer the following questions:

• Can shuttling capacity become an issue?
• What is the expected effect of further lockdown measures?
• Which intensive care capacity should exist in which place?
• Which group of the population should get priority for vaccinations?

Computationally, the model remains in the realm of linear programming (adding integrality restrictions adds very little to its accuracy), which means that huge and complex models of this kind can be solved in a short time.

Conclusions

We presented a successful application of Ab Ovo’s Network Designer functionality to the COVID-19 pandemic. Network Designer’s flexibility, its analysis functionalities, and the built-in optimizer capability were employed in a model of intensive care capacity, with an outlook, that answers to related questions could be obtained with relative ease as well.

More information

Interested in learning more? Please have a look at our Network Designer Solution Sheet and contact me with any questions or challenges you may have.

References

1. Aronson, Jay E., A Survey of Dynamic Network Flows, Annals of Operations Research, 1989, number 20, pp. 1—60.
2. Kermack, W.O. and McKendrick, A.G., A Contribution to the Mathematical Theory of Epidemics, Proceedings of the Royal Society, Aug 1, 1927, pp. 700—721, https://royalsocietypublishing.org/doi/pdf/10.1098/rspa.1927.0118
3. István Z. Kiss, Joel C. Miller, and Péter L. Simon, Mathematics of Epidemics on Networks – From Exact to Approximate Models, volume 46 in series Interdisciplinary Applied Mathematics, Springer International Publishing AG, 2017.